Новый математический аппарат может кардинально упростить исследования в медицине, нефтехимии и пищевой промышленности.
Его масштаб сравним с фундаментальными работами Смолуховского и Эйнштейна по теории диффузии и броуновского движения.
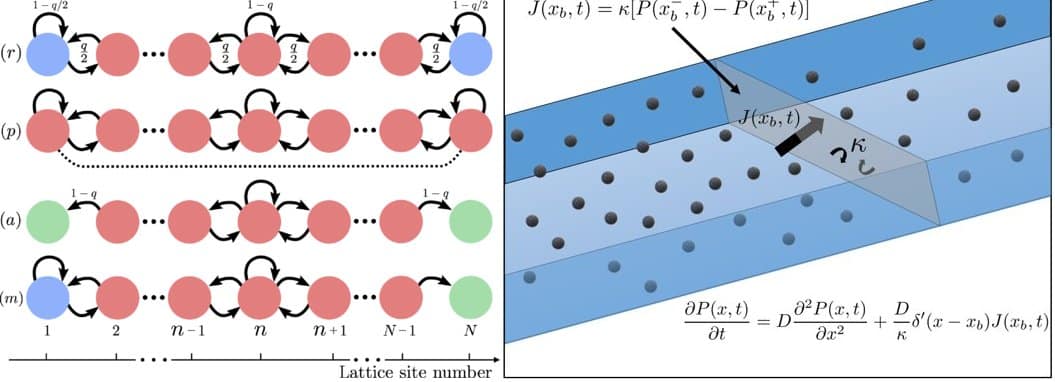
Специалисты Бристольского университета (Англия) предложили новое математическое описание движения веществ сквозь проницаемые материалы. С его помощью можно с высокой точностью моделировать распространение препаратов в живых тканях, движение газа и нефти в породах, устойчивость пищевой упаковки к проникновению инфекций и загрязнений. Работа английских математиков пока не опубликована, но уже прошла рецензирование в журнале Physical Review Research.
Диффузией называют движение атомов и молекул из области высокой концентрации микрочастиц в область низкой концентрации. Благодаря этому явлению газы и жидкости смешиваются, а твердые тела (например, металлы) при высоком давлении или долгом контакте «склеиваются» своими поверхностями. В целом, диффузия — это про то, как частицы вещества из-за броуновского (теплового) движения «толкаются» между собой и неизбежно разлетаются по всему доступному объему. Или смешиваются с частицами другого вещества.
Самый крупный вклад в современную теорию диффузии сделали Альберт Эйнштейн, Мариан Смолуховский и Жан-Батист Перрен в начале XX века. Их уравнения стали первой попыткой описать диффузию с точки зрения атомной теории строения вещества. Эти формулы уже более века используют для расчетов в области биохимии, добычи ископаемого топлива, очистки воды и промышленных стоков. Но они не описывают движение вещества в сложной среде, которая состоит из множества перегородок с разной проницаемостью. Например, распространение медицинского препарата в живой ткани с ее различными клеточными мембранами.
По словам Тоби Кея, специалиста по инженерной математике и ведущего автора работы, сейчас ученым приходится моделировать движение через каждую мембрану в отдельности, а потом собирать результаты в цельную картину. Это очень сложно и требует больших вычислительных ресурсов. Новое уравнение позволяет «в один заход» моделировать диффузионное движение через среду любой сложности и любого масштаба. Причем оно с одинаковой точностью описывает как распространение нефти в геологических пластах, так и миграцию животных через преграды вроде заборов и дорог.
Исследование английских математиков опирается на работу 2020 года, которую провела примерно та же команда ученых Бристольского университета. Тогда они решили 100-летнюю задачу математической физики, описав движение частицы в произвольной молекулярной решетке. Как говорит доктор Лука Джуджиоли, принявший участие в обоих исследованиях, значение той работы 2020 года до сих пор трудно оценить. Она дает очень глубокое понимание, по каким законам движется вещество на микроуровне, и таит в себе еще много ответов на самые захватывающие вопросы.
