В какую сторону будет вращаться обычный садовый опрыскиватель, если поток жидкости в нем обернуть вспять? Ответ на этот вопрос выглядит абсолютно очевидным. И он всегда разный в зависимости от степени понимания отвечающим физики протекающих процессов. Поэтому неудивительно, что загадка об инвертированном разбрызгивателе занимала лучшие умы человечества многие десятилетия. К счастью, американские ученые наконец-то теоретически и экспериментально обосновали по-настоящему правильное ее решение.

Для начала стоит упомянуть, что проблема инвертированного разбрызгивателя — наглядная иллюстрация закона Стиглера: Ричард Фейнман лишь популяризовал загадку, но сформулировал ее далеко не первым. Наиболее раннее упоминание этого теоретического вопроса встречается в труде The Science of Mechanics (1883 год) небезызвестного Эрнста Маха, именем которого названо число Маха. Экспериментальные попытки определить, в какую сторону будет вращаться инвертированный разбрызгиватель, стали предпринимать примерно с 1940-х годов.
Имя Фейнмана с этой задачей связано следующим образом. Во-первых, когда он услышал обсуждение проблемы инвертированного разбрызгивателя (как раз в 1940-е) коллегами-аспирантами, предложил провести эксперимент. И не где-нибудь, а в помещении циклотрона Принстонского университета. Опыт закончился феерично: задействованный в процессе стеклянный бак разорвало от избыточного давления. Результат оказался спорным, разбрызгиватель сначала немного дернулся вокруг своей оси, а затем замер и больше не двигался. Хотя вода через него продолжила проходить.
Во-вторых, именно Фейнман познакомил широкую публику с проблемой инвертированного разбрызгивателя. Она упоминается в его автобиографической книге «Вы, конечно, шутите, мистер Фейнман» (1985 год). Хотя в среде популяризаторов науки и ученых эта задача и ранее ассоциировалась с его фамилией, чем гениальный физик явно не был доволен. Он справедливо указывал, что лавры первооткрывателя принадлежат не ему, а Маху.
Упрощенно суть проблемы заключается в следующем. Полностью погрузим садовый S-образный вращающийся разбрызгиватель в большую емкость и попробуем откачать через него воду. В какую сторону будет вращаться разбрызгиватель и будет ли он это делать вообще? Возможных решений три:
- Он будет вращаться в сторону, противоположную «обычному» режиму разбрызгивания: вода же всасывается, следовательно, на срезе сопел возникает разрежение. Это объяснение наименее полное с точки зрения физики, но интуитивно кажется самым логичным.
- Он будет вращаться в ту же сторону, что и «обычный» разбрызгиватель: увлекаемая в него вода передает часть крутящего момента на изгибающееся сопло. Этот вариант требует как можно меньшего трения во всех вращающихся деталях разбрызгивателя.
- Он останется на месте: сила реакции сопла, всасывающего воду, уравновешивается моментом, который вода передает изгибу внутри сопла. С точки зрения большинства изучавших проблему ученых, это наиболее правильный вариант.

На протяжении последнего полувека различные исследователи проводили эксперименты, чтобы определить, какой из этих вариантов соответствует действительности. Но результаты были всегда неоднозначные. Даже в тех случаях, когда трение движущихся частей разбрызгивателя удавалось снизить практически полностью, он либо стоял на месте, либо едва заметно вращался в противоположную сторону. Полноценного ответа найти не получалось.
За решение эпохальной задачи взялась лаборатория прикладной математики Курантовского института математических наук (NYU Courant: Institute) — независимого подразделения Нью-Йоркского университета. В ней уже не раз отвечали на животрепещущие вопросы «жизни, Вселенной и вообще»: в 2018 году нашли рецепт идеальных мыльных пузырей, в 2021-м объяснили формирование загадочных каменных лесов, а в 2022-м изучили нюансы аэродинамики планеров с тончайшими крыльями (что позволяет делать самые эффективные бумажные самолетики). Новая научная работа плодотворной исследовательской организации опубликована в рецензируемом журнале Physical Review Letters.
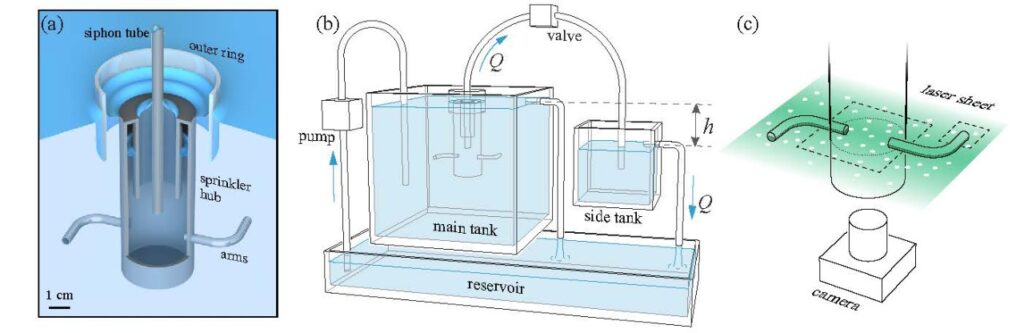
Чтобы во всех деталях изучить происходящее с инвертированным разбрызгивателем, ученым пришлось попотеть. Сначала они создали наиболее полную модель устройства, провели все необходимые вычисления и рассчитали разные варианты развития событий в эксперименте. Для опыта исследователи собрали такую установку, в которой не только минимизировано трение, но и устранены возможные возмущения от потоков жидкости вокруг самого разбрызгивателя.
Во время эксперимента использовали не обычную воду — в нее добавили отражающие микрочастицы, которые ярко светились в лучах подсвечивающего лазера. Так получилось наглядно увидеть поток жидкости и все возникающие в нем турбулентности. Результатом экспериментов и моделирования стала удивительная картина: инвертированный разбрызгиватель действительно будет крутиться в сторону, противоположную «обычному» режиму работы. Только в 50 раз медленнее. Самое удивительное, что обнаружили исследователи: механизм этого вращения полностью идентичен таковому у «правильного», не инвертированного разбрызгивателя. И его секрет кроется в том, что происходит внутри устройства.
Дело в том, что при всасывании воды, трубки-сопла тоже формируют струи, только не снаружи разбрызгивателя, а внутри. Даже если они расположены строго на противоположных сторонах кольца и оси их параллельны, получившиеся струи не обязательно столкнутся в центре. Ведь сопла изгибаются, меняют направление движения воды, а она, в свою очередь, получает от этого дополнительный импульс. И когда покидает трубку, часть этого импульса заставляет поток отклоняться от прямолинейной траектории.
В результате внутри разбрызгивателя возникает несколько вихрей, вращающихся в противоположные стороны. Но их размер, а вместе с тем скорость и объем вовлеченной воды, не одинаковый. Это приводит к неравномерному распределению момента силы в разных направлениях. И устройство вращается.
Вывод исследования можно кратко сформулировать так: будет ли фейнмановский разбрызгиватель вращаться и если да, то в какую сторону, — в первую очередь зависит от внутренней геометрии этого разбрызгивателя. В общем случае он будет едва заметно вращаться в обратную сторону, но если трение в его деталях велико, то это движение зафиксировать трудно.
