
Ученые после 32 лет исследований решили загадку девятого числа Дедекинда (23 цифры) с помощью суперкомпьютера Noctua. Открытие, для которого потребовались передовые вычислительные методы, проливает свет на до сих пор неизученный аспект монотонных булевых функций. Это демонстрирует потенциал суперкомпьютеров для решения сложных математических задач и открывает путь к новым исследованиям в этой области.
Некоторые математические загадки, описывающие нашу реальность, например золотое сечение, продолжают удивлять исследователей своей сложностью. Среди них есть математические сущности, вызвавшие интерес с момента открытия Рихардом Дедекиндом в конце 19 века. Некоторая часть сложных числовых задач касается «монотонных булевых функций», которые долгое время хранили свои секреты — восемь из них были решены лишь недавно. Проблема «девятого числа Дедекинда» остаётся неуловимой уже более трёх десятков лет, представляя собой серьёзную проблему для математиков.
Группа учёных из Университета Падерборна и университета Лёвена с помощью суперкомпьютера Noctua раскрыла тайну. Результаты, полученные после многолетних исследований и расчетов, являются важным шагом в математике и открывают возможности для решения сложных задач. Отчёт о работе будет представлен в сентябре на международном семинаре по булевым функциям и их приложениям в Норвегии.
Числа Дедекинда — сложное понятие
Числа Дедекинда представляют собой уникальные математические величины. целые числаЦентральное значение в изучении монотонных булевых функций имеют вычисления, основанные на математической логике с двоичными значениями: 0 и 1 или истина и ложь. В контексте чисел Дедекинда эти функции определяют выход из множества двоичных входных данных.
Монотонные булевы функции представляют собой подмножество булевых функций. Их особенность заключается в том, что замена нуля на единицу на входе приводит только к изменению выхода с нуля на единицу, но не наоборот. Эти функции «монотонны» потому, что после изменения значения с нуля на единицу его нельзя изменить обратно.
Леннарт Ван Хиртум, главный автор исследования, говорит в сообщении для прессы: Монотонную булеву функцию в двух, трех или n измерениях можно представить как игру с n-мерным кубиком. Вы балансируете кубик на одном углу и окрашиваете каждый из оставшихся углов в белый или красный цвет. Единственное правило — никогда не ставить белый угол на красный. Это образует красно-белое вертикальное пересечение. Цель игры — подсчитать количество различных вариантов. Число вариантов известно как число Дедекинда. Даже если это не сразу заметно, числа во время игры быстро становятся огромными: 8-е число Дедекинда уже состоит из 23 цифр. «.
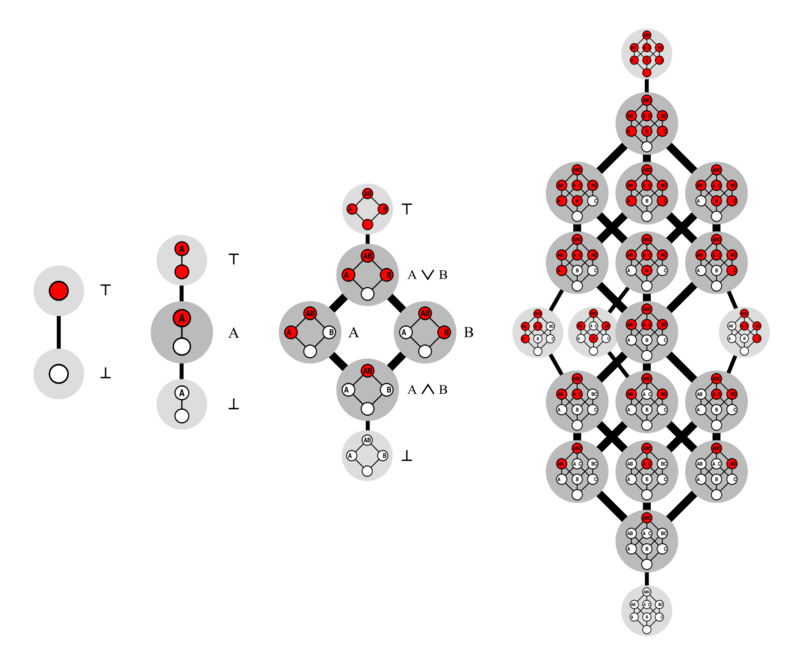
Эти функции крайне важны в разных разделах математики и компьютерных наук, особенно при исследовании структур данных, алгоритмов и теории графов.
Решение математической загадки
Открытие Д(9) Дедекинда состоялось 9 числа благодаря передовым вычислительным методам и мощному суперкомпьютеру Noctua. Для решения задачи исследователи применили формулу коэффициента P.
Формула предлагает вычислить числа Дедекинда, складывая большое количество чисел. Это позволило вычислить D(8) за восемь минут на обычном ноутбуке. Но вычисление D(9) займет сотни тысяч лет даже на мощном суперкомпьютере.
Для достижения цели исследователям пришлось использовать высокоспециализированные параллельные арифметические устройства, называемые FPGA. Ван Хиртум создал первый прототип аппаратного обеспечения для ускорения определённых вычислений. После этого учёные обратились к суперкомпьютеру Noctua 2 в Падерборнском центре параллельных вычислений при университете Падерборна, обладающему одной из самых мощных систем FPGA в мире.
Важное открытие
Разработанная в течение нескольких лет программа проработала на суперкомпьютере около полугода. 8 марта 2023 года учёные обнаружили девятое число Дедекинда: 286386577668298411128469151667598498812366. Это открытие свидетельствует о впечатляющей мощности суперкомпьютеров и передовых методов вычислений.
Эти машины способны выполнять миллиарды вычислений за секунду, применяя большие объемы данных. Это делает их незаменимыми для решения сложных математических задач, например, девятого числа Дедекинда. Передовые методы вычислений позволяют структурировать и оптимизировать эти операции, чтобы полностью использовать возможности суперкомпьютеров.
Это открытие не только демонстрирует возможности суперкомпьютеров и передовых методов вычислений, но и открывает путь для новых исследований и открытий в математике. Решение девятого числа Дедекинда может привести к лучшему пониманию монотонных булевых функций и их применению в разных областях, начиная от информатики и заканчивая логикой.