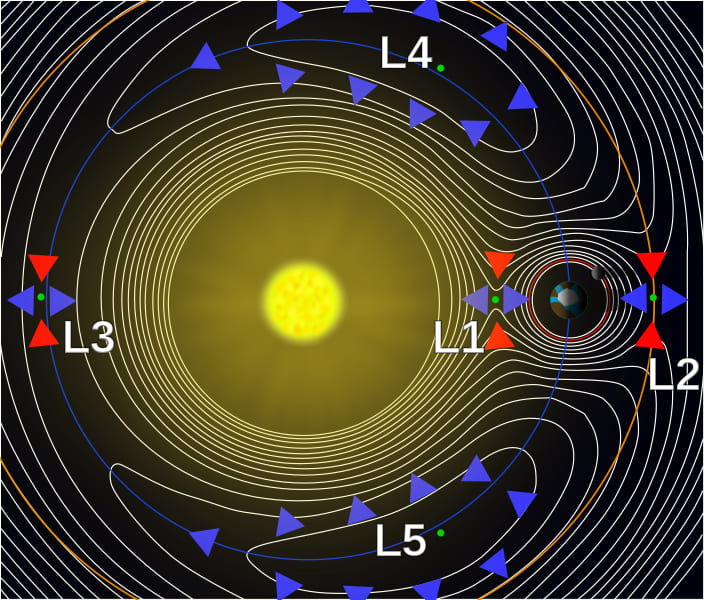
Точки Лагранжа — это области равновесия, где совместное гравитационное поле двух массивных тел уравновешивается центробежной силой, действующей на значительно более лёгкий объект, вследствие чего этот объект находится в покое относительно двух больших тел.
Предистория терраформирования Марса или Луны для жизни людей уходит корнями в 1970-е годы, когда энтузиасты космических поселений заинтересовались идеей орбитальных колоний. Физик Джерард О’Нил выдвинул концепцию среды обитания, которая будет находиться в относительно стабильных точках космоса — точках Лагранжа.
Если бы удалось обнаружить подходящее положение между Луной и Землёй, то в нём можно было бы разместить объект небольшого веса, который будет вращаться вокруг Земли синхронно с Луной неограниченно долгое время.
Что такое точки Лагранжа?
Гравитация двух крупных объектов в одной точке пространства редко уравновешивается, из-за чего меняется траектория каждого из них.
Точки Лагранжа — области равновесия, где суммарное гравитационное поле двух массивных объектов компенсирует силу центробежия, действующую на третий, значительно менее массивный объект. Чистая сила на этот объект равна нулю.
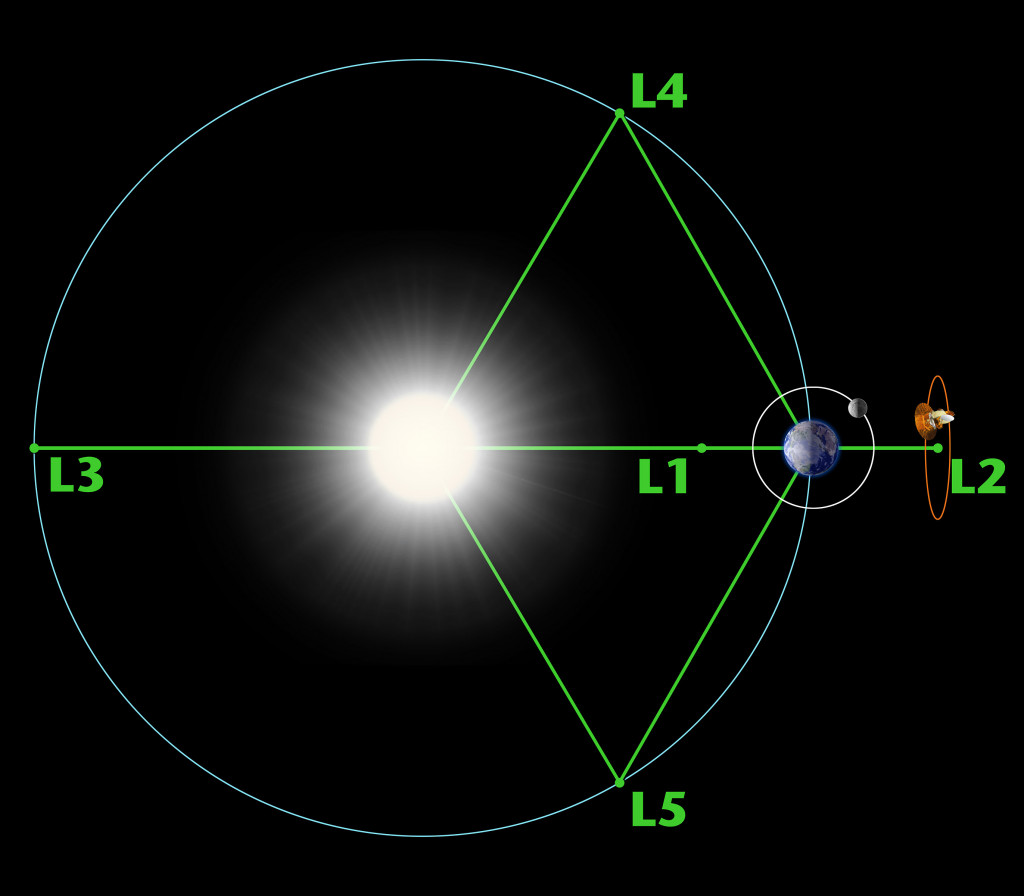
Достигнув точки равновесия, маломассивный объект получит нулевую массу и ускорение по сравнению с более тяжелыми телами, оставаясь в покое. Рядом с звездой или небесным телом существуют пять точек, где все силы уравновешены.
Эти точки, ещё называемые точками равновесия, не имеют постоянного местоположения в пространстве, но остаются неизменными относительно двух главных тел. Для системы «Земля-Луна» эти точки движутся вместе с центром тяжести Земли и Луны тем же периодом, что и Луна.
Математика, разрешившая задачу трёх тел.
Пока только Земля и Луна сходятся, Луна следует необычному пути, вычисляемому с высокой точностью математическими формулами. Что же случается, если вмешательство окажет третья планета?

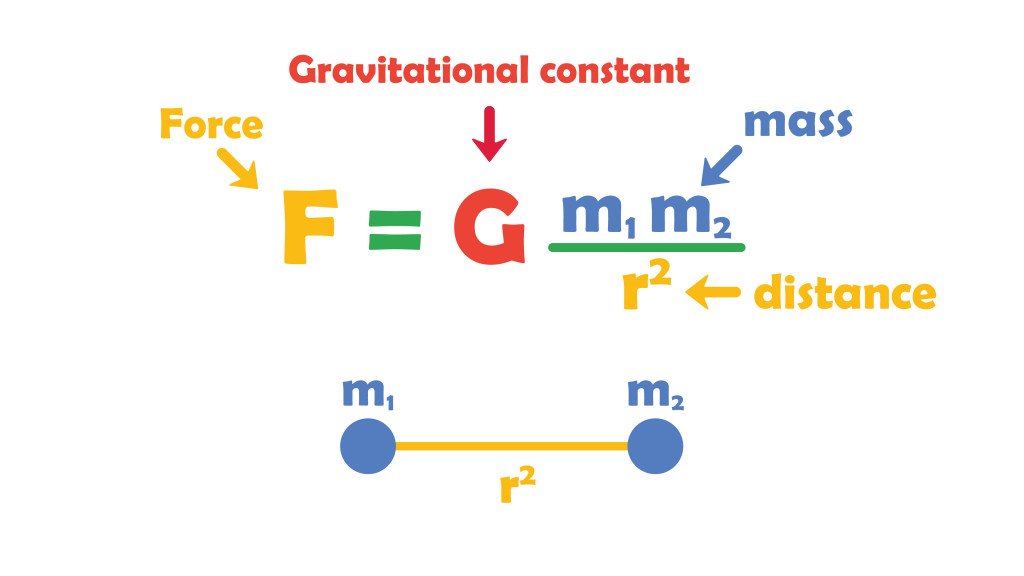
Задача трёх тел состоит в определении местоположения трёх небесных тел, взаимодействующих гравитацией (сила обратного квадрата), относительно друг друга во времени (движения). Из-за множества сил, действующих на объекты в пространстве, система из трёх тел в итоге становится хаотичной, и точное поведение тел невозможно предсказать.
Ньютону удалось получить общее решение для задачи о двух телах, в то время как задача о трёх телах оказалась куда более трудной. С появлением третьего тела проблема значительно усложнилась. Исследования Пуанкаре показали, что детерминированного решения задачи трех тел может и не существовать.
Гравитация уменьшается с расстоянием, поэтому сила притяжения сильнее для объектов, находящихся ближе, чем для тех, что находятся дальше. Этот принцип помог создать упрощенные модели, например ограниченное приближение трех тел, где учитываются только две наиболее массивные тела в системе.
Точки Лагранжа — специальные решения задачи трех тел, когда одно тело существенно меньше двух других.
В силу большей массы Земля оказывает более сильное гравитационное воздействие на объекты по сравнению с Луной. На третье тело (масса которого незначительна по сравнению с массой главных тел и не оказывает заметного влияния на их движение), находящееся между этими двумя телами, будут действовать силы со стороны каждого из них.
Камень между Землей и Луной подвергается притяжению обеих небесных тел. Земля, имея большую массу, действует на него сильнее, но сила тяжести ослабевает с увеличением расстояния. Чем дальше камень от Земли, тем слабее это притяжение.
Достигается момент, когда земное притяжение сравнивается с лунным, и камень ощущает нулевую чистую гравитационную силу. Эта точка, гравлтационно-нейтральная, представляет собой место, где объект без скорости будет пребывать и не падать ни к Земле, ни к Луне.
По мере сближения с Луной за пределом этой точки, лунная гравитация станет доминирующей силой, и объект начнет устремляться к Луне. Дальнейшее отдаление объекта от этой точки приведет к обратной тяге — он будет притягиваться обратно к Земле.
Гравитационно нейтральную точку иногда ошибочно называют точкой Лагранжа (точнее L1). Такое заблуждение возникает из-за того, что существование такой точки теоретически предполагает статичность двух тел, для которых она определяется – Земли и Луны.
Однако это вовсе не так! Земля с Луной вращаются вокруг общего центра тяжести, постоянно двигаясь и создавая центробежную силу. Эта сила, по сути, отбрасывает объекты в космос во время их движения по орбитам.
Движение Земли и Луны порождает пять точек равновесия, где гравитация и центробежная сила уравновешиваются. Такой же принцип применим к любой системе из трёх тел, при условии m3<
Линии L1, L2 и L3 коллинеарны и располагаются на одной прямой. Линия L1 находится между двумя телами; линия L2 расположена на той же линии, но за меньшим из двух тел. Линия L3 также расположена на той же линии, но позади большего из двух объектов. Линии L4 и L5 проходят через третью вершину равносторонних треугольников, основанием которых служат две основные массы системы.
Посмотрим ещё раз на систему Земля-Луна. Три из пяти точек Лагранжа находятся на линии между центрами Земли и Луны. Первая точка, L1, расположена между Землёй и Луной, где совместное действие гравитации двух тел создаёт равновесие, немного ближе к Земле, чем нейтральная гравитационная точка.
L2 располагается дальше от Луны, за ее обратной стороной. L3 находится на противоположной стороне, за пределами Земли. Для L2 и L3 силы притяжения Земли и Луны равновесие центробежной силе позволяют объекту совершить оборот вокруг Земли за тот же период времени, что и Луна.
Точки L4 и L5 являются точками, где находятся третья вершина равностороннего треугольника, образованного центром Земли и центром Луны.
Все ли точки устойчивы?
Не все равновесные состояния устойчивы. Точки L4 и L5 сохраняют устойчивость при условии, что отношение масс двух крупных тел больше 24,96. Это требование выполняется для систем Земля-Солнце, Земля-Луна и Солнце-Юпитер. Поскольку масса Земли примерно в 81 раз превышает массу Луны, а масса Солнца более чем в 1000 раз больше массы Юпитера, точки L4 и L5 вращающихся систем Земля-Луна и Солнце-Юпитер являются стабильными.
Точки L1, L2 и L3 нестабильны по своей природе. Оставление объекта в этих точках подобно балансировке шара на холме: при точном размещении он сохранит свое положение. Но любое отклонение приведет к смещению. Таким образом, объекту в любой из неустойчивых точек понадобится помощь для удержания его в «идеальном» месте.
Если объект отклоняется от точки равновесия, его положение нарушается, и он колеблется вокруг этой точки по траекториям, называемым либрациями. Каждая точка Лагранжа имеет область, где тело может находиться с небольшим запасом. Космический корабль, вращающийся вокруг определенной точки Лагранжа, фактически движется в пределах одной из таких областей, имеющих форму «островных орбит». Размер каждого острова разный.
Космические миссии в точках Лагранжа

Солнечная гелиосферная обсерватория (SOHO), Авансированный исследователь состава (ACE) и Глобальная геогеология WIND располагаются на орбите вокруг точки L1 Солнца-Земля, что обеспечивает постоянное и непрерывное наблюдение Солнца. Это делает её идеальным местом для изучения солнечной среды. В отличие от SOHO, ранее существующие солнечные обсерватории, вращавшиеся вокруг Земли, прерывали наблюдения всякий раз, когда Земля затмевала Солнце, перекрывая его из поля зрения.
Космический зонд WMAP, предназначенный для изучения свойств ранней Вселенной по данным о космическом микроволновом фоновом излучении, был развёрнут в точке Лагранжа L2 Солнце-Земля (2001–2010 гг.), но вместо закрепления на данной позиции он совершал другие движения. .
Космический телескоп Джеймса Уэбба (JWST) в точке L2 Солнца-Земли и климатическая обсерватория глубокого космоса (DSCOVR) в точке L1 могут функционировать там с минимальным расходом топлива и незначительными корректировками. В то же время другие космические обсерватории, такие как «Гершель» и «Планк» (для предельно точного измерения CMB), а также «Гайя» (для картирования положения и скоростей миллиарда звезд с целью изучения истории Млечного пути), находятся на орбите Солнце-Земля L2.
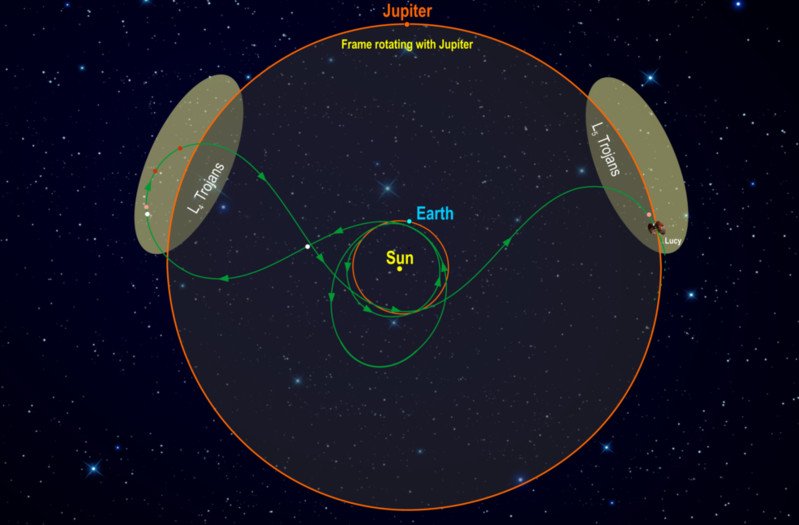
Более семи тысяч астероидов вращаются вокруг гравитационно устойчивых точек Лагранжа L4 и L5 в системе Солнце-Юпитер. Названные троянцами, эти небесные тела преимущественно разделены на два скопления — одно предшествует газовому гиганту, другое следует за ним по орбите вокруг Солнца.
Исследователи считают, что области Лагранжа могут скрывать ненайденные планеты или фрагменты старых внеземных кораблей. Если космический корабль мог создавать силу, противодействующую гравитации, можно было бы создать искусственные точки равновесия, где он мог оставаться практически в любой точке космоса без постоянного следования по орбите. Для этого подойдут солнечные паруса, использующие свет Солнца для движения.
Миссии к точкам Лагранжа служат платформами для углубления космического исследования.